『聚合』你的DDPG/RDPG为何不收敛？

园子好多年没有更过了，草长了不少。上次更还是读博之前，这次再更已是博士毕业2年有余，真是令人唏嘘。盗链我博客的人又见长，身边的师弟也问我挖的几个系列坑什么时候添上。这些着实令我欣喜，看来我写的东西也是有人乐意看的。去年11月份左右，因为研究需要，了解了一下强化学习（Reinforcement learning）。没想到这一了解就花了我10个月，看来我又得开新坑了。最近几个月亲自实践了多种高阶的强化学习算法。实践的过程毫无疑问是痛苦的，我的自信心被某些“细节”反复搓揉，待我决定写这篇Blog的时候，自信心已经被搓的稀巴烂了。我一贯喜欢在趟雷之后写Blog，防止被我踩过的雷再崩到别人。如果你此刻也在被DDPG/RDPG的某些细节搓揉，希望这篇博客能帮到你。

根据个人经历，我把强化学习的学习过程分为几个层次：

第一层次：RL小白（症状：误以为RL和DL’深度学习’没什么区别，不过换个算法罢了）

第二层次：学习了RL的基本概念，逐渐抓住RL的本质（序贯决策），但从未运行过RL的程序

第三层次：掌握了RL的大部分主干算法和逻辑，运行过别人写的RL程序，以为对RL懂得很多了。

第四层次：亲自实践RL的程序，并应对多种不同的类型的Environment，然后惊讶的发现“CNM，为毛算法不收敛？难道我学习的理论错了？难道我的程序错了？”

如果你处于第一个层次或者第二个层次，建议你转去莫烦Python或者是刘建平Pinard补基础。

如果你处于第三个层次，劝君一句话：“纸上得来终觉浅，觉知此事要躬行”。RL的细节不是一般的多，而且招招致命。这一点和ML/DL真不太一样。

如果你处于第四个层次，这篇文章希望成为你的答案。

本文分为四个部分：

DDPG不收敛的潜在原因分析
RDPG不收敛的潜在原因分析（含Github上几个不能收敛的RDPG源码分析）
D(R)DPG可以收敛的源码（分Keras和pytorch两种版本）
强化学习实践（编程）过程的几点建议

一：DDPG不收敛的潜在原因分析

先上DDPG的算法伪代码：

（1）在编写Q(s, a)的过程中，错误的使用了layer.Add层而非layer.concatenate (keras版)或torch.cat (pytorch版)

会导致不收敛的critic代码如下：

 #程序清单1
 1 from keras.layers import Add
 2 #如下代码定义了critic网络
 3 def _build_critic(self, featureDim, actionDim, learningRate=LR_C):
 4         stateInputs = Input(shape = (featureDim, ), name = 'State-Input')
 5         actionInput = Input(shape = (actionDim, ), name = 'Action-Input')
 6         stateOut = Dense(30, activation = 'relu')(stateInputs)
 7         actionOut = Dense(30, activation = 'relu')(actionInput)
 8         Outputs = Add()([stateOut, actionOut])
 9         init = RandomUniform(minval = -0.003, maxval = 0.003)
10         Outputs = Dense(1, activation = 'linear', name = 'Q-Value', kernel_initializer = init)(Outputs)            
11         critic = Model(inputs = [stateInputs, actionInput], outputs = Outputs)
12         return critic

不收敛原因的分析：写代码的时候一定要多想想Q(s, a)的本质是什么？Q(s, a)的本质是多键值的联合查表，即采用s和a作为键值在一个表格中查表，只不过这个表格用神经网络替代了。也就是说，作为键值，s和a一定要分别单独给出，而不能加在一起然后再给神经网络。

可以收敛的critic写法如下（Keras版）：

#程序清单2
 1 from keras.layers import concatenate
 2 
 3 def _build_critic(self, featureDim, actionDim, learningRate=LR_C):
 4 
 5         sinput = Input(shape=(featureDim,), name='state_input')
 6         ainput = Input(shape=(actionDim,), name='action_input')
 7         s = Dense(40, activation='relu')(sinput)
 8         a = Dense(40, activation='relu')(ainput)
 9         x = concatenate([s, a])
10         x = Dense(40, activation='relu')(x)
11         output = Dense(1, activation='linear')(x)
12 
13         model = Model(inputs=[sinput, ainput], outputs=output)
14         model.compile(loss='mse', optimizer=Adam(lr=learningRate))
15 
16         return model

（2）如果采用PyTorch编写actor神经网络，有一点要注意（经笔者实验，只有PyTorch有这个问题，Keras的coder可以放心的跳过这一节了）

使用PyTorch尽量不要使用Lambda层，实验结果上来看它似乎非常影响收敛性。尽管Keras上使用Lambda层不影响收敛性。

会导致收敛过程很坎坷甚至不收敛的actor代码如下：

#程序清单3
 1 class Actor(torch.nn.Module):
 2     def __init__(self, s_dim, a_dim):
 3         super(Actor, self).__init__()
 4         self.Layer1 = torch.nn.Linear(s_dim, 30)   # Input layer
 5         self.Layer2 = torch.nn.Linear(30, 30)
 6         self.Layer3 = torch.nn.Linear(30, a_dim)
 7         self.relu = torch.nn.ReLU()
 8         self.tanh = torch.nn.Tanh()
 9 
10     def forward(self, s_input):
11         out = self.relu(self.Layer1(s_input))          # linear output
12         out = self.relu(self.Layer2(out))
13         out = self.tanh(self.Layer3(out))
14         out = Lambda(lambda x: x * 2)(out)
15         return out

注意到程序的第14行引用了Lambda层，笔者当时解决的问题是“Pendulum-v0”，对于该问题，合法的动作空间是[-2, 2]之间的。而13行的tanh输出在[-1, 1]之间。所以需要把13行的输出乘以2。但是笔者发现，这种写法收敛的过程相较不采用Lambda层而直接将out乘以2（代码之后给出）输出收敛的更慢，并且收敛的过程会被反复破坏然后再收敛，如下图：

上图的蓝线表示critic_loss, 橘线表示实时动作-状态值函数的预测输出。可以从上图（左）看到，在PyTorch中采用Lambda层规范动作值使得critic对动作-状态值函数的预测难以收敛，这表示它对critic的预测带来了负面的影响，总是不断的破坏critic的收敛性。上图（右）的代码如程序清单4中所示。直接将上一层网络的输出乘以2而没有使用Lambda层。可见critic的预测可以逐渐趋近于0（对于Pendulum-v0这是收敛，其他环境不趋于0），收敛性也好了很多。

可以收敛的actor写法如下：

#程序清单4
 1 class Actor(torch.nn.Module):
 2     def __init__(self, s_dim, a_dim):
 3         super(Actor, self).__init__()
 4 
 5         self.l1 = torch.nn.Linear(s_dim, 40)
 6         self.l2 = torch.nn.Linear(40, 30)
 7         self.l3 = torch.nn.Linear(30, a_dim)
 8 
 9     def forward(self, x):
10         x = F.relu(self.l1(x))
11         x = F.relu(self.l2(x))
12         x = 2 * torch.tanh(self.l3(x))
13         return x

（3）如果采用PyTorch编写critic神经网络，有一点要注意（经笔者实验，也是只有PyTorch有这个问题，Keras的coder可以放心的跳过这一节了）

在编写Q(s, a)的时候，s和a一定要在一开始输入神经网络的时候就做连接操作（上文提到的concatenate）而不要让s和a分别经过一层神经网络后再做连接操作。否则，critic会不收敛。

会导致不收敛的critic代码如下：

#程序清单5 
1 class Critic(torch.nn.Module):
 2     def __init__(self, s_dim, a_dim):
 3         super(Critic, self).__init__()
 4         self.Layer1_s = torch.nn.Linear(s_dim, 30)
 5         self.Layer1_a = torch.nn.Linear(a_dim, 30)
 6         self.Layer2 = torch.nn.Linear(30+30, 30)
 7         self.Layer3 = torch.nn.Linear(30, 1)
 8         self.relu = torch.nn.ReLU()  
 9         
10     def forward(self, s_a):
11         s, a = s_a
12         out_s = self.relu(self.Layer1_s(s))
13         out_a = self.relu(self.Layer1_a(a))
14         out = self.relu(self.Layer2(torch.cat([out_s, out_a], dim=-1)))
15         out = self.Layer3(out)
16         return out

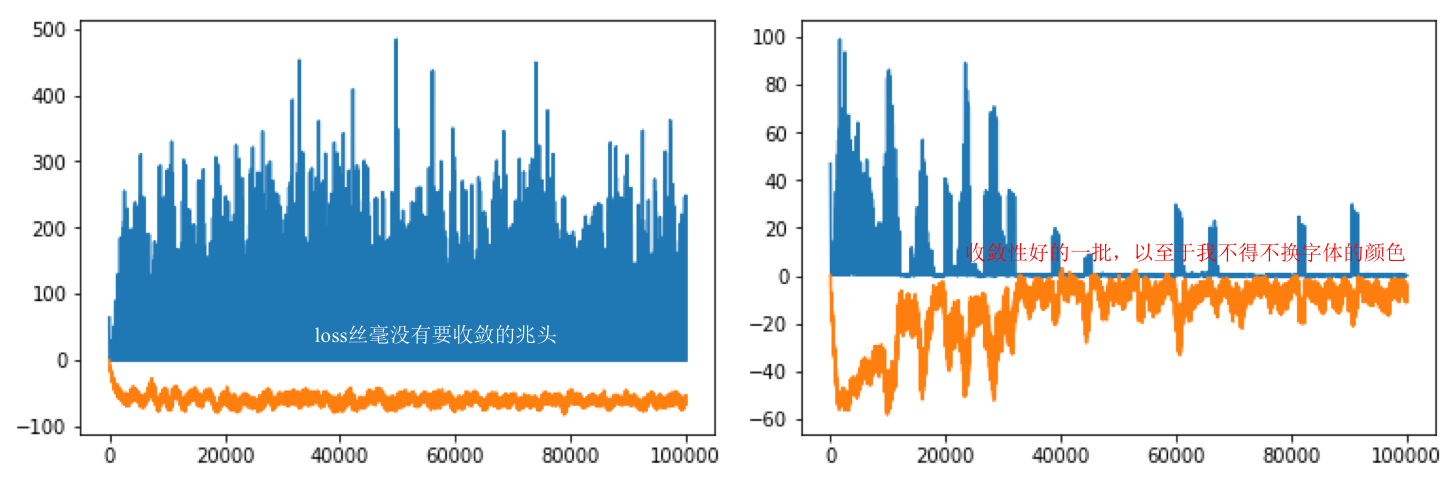
上图的蓝线表示critic_loss, 橘线表示实时动作-状态值函数的预测输出。上图（左）是程序清单5运行的结果输出。上图（右）是程序清单6运行的结果输出。

可以收敛的critic写法如下：

#程序清单6 
 1 class Critic(torch.nn.Module):
 2     def __init__(self, s_dim, a_dim):
 3         super(Critic, self).__init__()
 4 
 5         self.l1 = torch.nn.Linear(s_dim + a_dim, 40)
 6         self.l2 = torch.nn.Linear(40 , 30)
 7         self.l3 = torch.nn.Linear(30, 1)
 8 
 9     def forward(self, x_u):
10         x, u = x_u
11         x = F.relu(self.l1(torch.cat([x, u], 1)))
12         x = F.relu(self.l2(x))
13         x = self.l3(x)
14         return x

⚠ 文章源地址: https://www.cnblogs.com/hdu-zsk/p/11328295.html 转载请注明出处

目录CONTENT

『聚合』你的DDPG/RDPG为何不收敛？

评论区

『聚合』 你的DDPG/RDPG为何不收敛？

评论区

『聚合』你的DDPG/RDPG为何不收敛？