k-均值聚类算法（英文：k-means clustering）

定义：
k-均值聚类算法的目的是：把n个点（可以是样本的一次观察或一个实例）划分到k个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准。

Background Knowledge Introduction

K-Means 是发现给定数据集的 K 个簇的聚类算法, 之所以称之为 K-均值是因为它可以发现 K 个不同的簇, 且每个簇的中心采用簇中所含值的均值计算而成。
簇个数 K 是用户指定的, 每一个簇通过其质心（centroid）, 即簇中所有点的中心来描述。

术语介绍：

簇: 所有数据的点集合，簇中的对象是相似的。
质心: 簇中所有点的中心（计算所有点的均值而来）.
SSE: Sum of Sqared Error（误差平方和）, 它被用来评估模型的好坏，SSE 值越小，表示越接近它们的质心. 聚类效果越好。由于对误差取了平方，因此更加注重那些远离中心的点（一般为边界点或离群点）。详情见kmeans的评价标准。

有关簇和质心术语的图形介绍, 请参考下图:

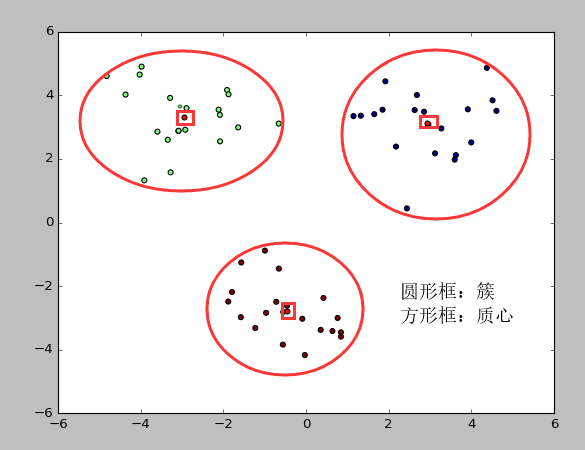
公式介绍：
已知观测集(x1,x2,…,xn)，其中每个观测都是一个 d-维实向量，算法要把这 n个观测划分到k个集合中(k≤n)，使得组内平方和最小。
换句话说，它的目标是找到使得下式满足的聚类Si，

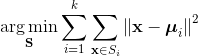
其中 μi 是Si 中所有点的均值。

其中:

arg min表示我们要最小化后面的那个表达式。
k是我们要找到的聚类的数量。
∑∑是双重求和符号,表示我们要对所有的数据点和所有的聚类进行求和。
||x - μi||^2表示数据点x与第i个聚类中心μi之间的欧几里得距离的平方。

整个公式的意思是:

我们要找到k个聚类中心，使得所有数据点到它们所属聚类中心的总距离的平方和最小。
K-Means算法的目标就是将数据点划分到不同的聚类中，使得每个数据点与它所属的聚类中心之间的距离尽可能小，从而最小化整个目标函数。
通过最小化这个目标函数，我们可以得到比较紧密的聚类，数据点在同一个聚类内部是相对聚集的，而不同聚类之间是相对分散的。这样的聚类结果通常被认为是比较合理和有意义的。
需要注意的是，由于K-Means算法的目标函数是非凸的，因此存在多个局部最小值。算法通过迭代优化的方式寻找一个相对比较好的局部最小值作为最终结果，但不能保证得到全局最优解。

这部分需要一定的数学基础，不懂的，可以跳过了，现在框架帮忙实现了这个公式，你要做的就是输入观测集(x1,x2,…,xn)而已。

Application Scenarios

kmeans，用于数据集内种类属性不明晰，希望能够通过数据挖掘出或自动归类出有相似特点的对象的场景。其商业界的应用场景一般为挖掘出具有相似特点的潜在客户群体以便公司能够重点研究、对症下药。

例子1: 产品部门的市场调研场景。为了更好的了解自己的用户，产品部门可以采用聚类的方法得到不同特征的用户群体，然后针对不同的用户群体可以对症下药，为他们提供更加精准有效的服务。

例子2: 生产部门的自动化场景。先采集产品的数据，预先标记出好产品的Key和坏产品的Key,通过聚类的方法就可以得到不同特征的产品群体。

Process

1. 创建 k 个点作为起始质心（通常是随机选择）;
2. 当任意一个点的簇分配结果发生改变时（不改变时算法结束）;
    2.2. 对数据集中的每个数据点;
          2.2.1. 对每个质心;
              2.2.1.1. 计算质心与数据点之间的距离;
          2.2.2. 将数据点分配到距其最近的簇;
    2.3. 对每一个簇, 计算簇中所有点的均值并将均值作为质心;

案例——区分好坏苹果（指定Key）

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import numpy as np

# 生成随机样本数据
# 假设你采集数据是二维的,每个样本有两个特征  [光泽, 气味]
appleData = np.array([[44, 40], [60, 45], [59, 70], [65, 80], [50, 50],
                      [75, 65], [45, 52], [64, 75], [65, 70], [53, 45]])

# 将样本分成2类 : 好果、坏果
# 设置两个初始簇中心的位置，指定Key值
initial_centroids = np.array([[40, 20], [70, 80]])

# 创建KMeans对象,并指定初始簇中心位置
kmeans = KMeans(n_clusters=2, init=initial_centroids)
kmeans.fit(appleData)

# 获取每个样本的类别
labels = kmeans.labels_

# 提取聚类中心
centroids = kmeans.cluster_centers_

# 绘制散点图并着色
colors = ['g', 'r']
for i in range(len(appleData)):
    plt.scatter(appleData[i][0], appleData[i][1], color=colors[labels[i]])

# 绘制聚类中心
for c in centroids:
    plt.scatter(c[0], c[1], marker='x', s=150, linewidths=5, zorder=10)

# 添加标签和标题
plt.xlabel('Glossiness')
plt.ylabel('Smell')
plt.title('Apple glossiness and smell K-Means clustering results')

# 显示图形
plt.show()

show

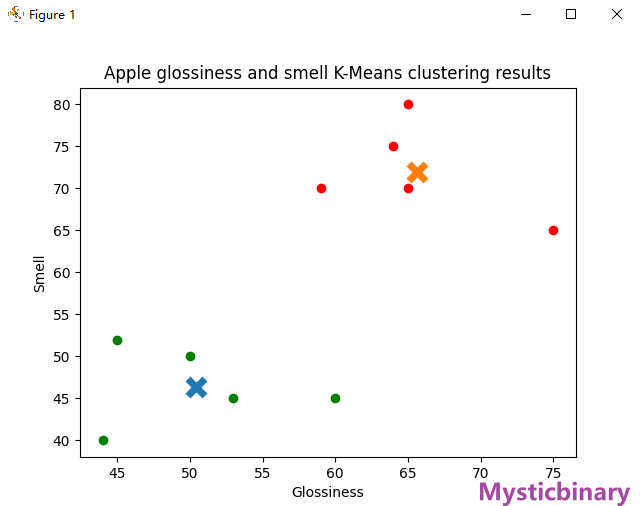
案例——自动聚类（随机Key）

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import numpy as np

# 生成随机样本数据
X = np.array([[60, 75], [59, 70], [65, 80], [80, 90], [75, 65],
              [62, 75], [58, 68], [52, 60], [90, 85], [85, 90],
              [70, 75], [65, 70], [55, 65], [75, 80], [80, 85],
              [65, 75], [60, 70], [55, 60], [95, 95], [90, 90]])

# 将样本分成3类
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

# 获取每个样本的类别
labels = kmeans.labels_

# 提取聚类中心
centroids = kmeans.cluster_centers_

# 绘制散点图并着色
colors = ['r', 'g', 'b']
for i in range(len(X)):
    plt.scatter(X[i][0], X[i][1], color=colors[labels[i]])

# 绘制聚类中心
for c in centroids:
    plt.scatter(c[0], c[1], marker='x', s=150, linewidths=5, zorder=10)

# 添加标签和标题
plt.xlabel('Glossiness')
plt.ylabel('Smell')
plt.title('Apple glossiness and smell K-Means clustering results')

# 显示图形
plt.show()

show